Lección 28 Complementación de trinomio cuadrado
perfecto
Existe una manera de lograr trinomios
cuadrados perfectos a partir de binomios si simplemente les sumamos y restamos
el termino que le haga falta.
1. Si tenemos un binomio cuyos dos factores tengan raíces cuadradas se siguen los siguientes pasos para la creación de un trinomio cuadrado perfecto:
1. Si tenemos un binomio cuyos dos factores tengan raíces cuadradas se siguen los siguientes pasos para la creación de un trinomio cuadrado perfecto:
- Se les extrae la raíz cuadrada a los dos términos.
- Se encuentra el doble producto de estas raíces.
- Este doble producto se suma y se resta a los dos términos que son cuadrados perfectos.
Ejemplo:
2. Si tenemos un binomio de la forma
x2 + bx hace falta completarlo con el cuadrado de la mitad del coeficiente de
la raíz del termino de la derecha.
Ejemplo:
Pero para que el resultado original
del polinomio no varíe se le debe restar lo mismo que se suma.
Ver vídeo:
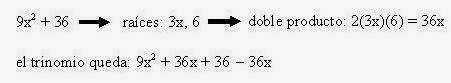

No hay comentarios:
Publicar un comentario